IV. Моделирование условнорефлекторной деятельности

Любой автомат, работающий по стандартной программе, может служить моделью безусловнорефлекторного (инстинктивного) поведения животного. Для моделирования адаптивного поведения типа условных рефлексов используются пластические логические элементы или элементы памяти и ассоциации. К настоящему времени создано большое количество моделей, игрушек и специальных устройств для демонстрации и моделирования различных форм поведения, вроде "черепахи" Грея Уолтера (обзор этих работ был выполнен Гаазе-Раппопорт, 1961).

Одной из интересных работ в области моделирования безусловного рефлекса является статья Калбертсона (1956). Он рассматривает гипотетическое устройство "робот без памяти", выполненное из искусственных нейронов трех типов: 1) рецепторные нейроны получают сигналы из внешней среды, которые подаются на 2) центральные нейроны, откуда, в свою очередь на 3) эффекторные нейроны, воздействующие на внешнюю среду.

Принципы соединения нейронов и условия их возбуждения аналогичны тем, какие постулируются в теории нервных сетей. Основная идея Калбертсона состоит в том, что, если бы мы имели соответствующие рецепторные и эффекторные элементы, а также неограниченное число центральных клеток и синапсов, то можно было бы построить работы, действующие в любой внешней среде, по любой заданной программе. Далее автор описывает другое устройство - "полный робот", или робот с полной памятью, где происходит сохранение следов всех событий - внешних воздействий и внутренних состояний - с момента возникновения автомата. По мнению автора, такой неэкономичный полный робот может повторять (по предписанию) любую деятельность, в том числе и человеческую как частный случай.

Приблизительно оценивая сложность такого устройства, как крайнюю, Калбертсон ставит задачу: как конструировать автоматы с промежуточным, заданным биологически, комплексным поведением, подражая экономной природе? Какой должна быть конструкция мозга, направляющего человеческую деятельность с помощью лишь 10¹⁰ клеток? По-видимому, одним из решений этой проблемы является наличие свойства пластичности нервной системы - изменение логической структуры ее организации в зависимости от цели или задачи текущей деятельности. Необходимым элементом модели условного рефлекса (временной связи) должно быть накопительное (запоминающее) устройство, или счетчик времени и событий (обзор технических конструкций запоминающих устройств различного типа можно найти в работе Крайзмера, 1962).

Различают постоянную (фиксированную), оперативную (кратковременную) и разнообразные промежуточные виды памяти. Для моделирования временной связи наиболее удобными оказываются инерционные элементы (нагревательный элемент - нагревание и остывание, электрическая емкость - заряд и разряд) и некоторые самоподдерживающиеся динамические процессы (реверберация волн и т. п.).

Рассмотрим работу часто применяемого в различных технических моделях живых организмов емкостного накопительного элемента, представляющего собой интегрирующую ячейку с постоянной времени заряда τ₁ = R₁C и разряда τ₂ = R₂C (рис. 88, A). Здесь возбудимость биологической системы моделируется уровнем электрического напряжения u_с на конденсаторе (Б), изменяющимся при поступлении прямоугольных импульсов (В) на входе 1-1 системы (А). Во время замыкания контакта К происходит относительно быстрый заряд (через сопротивление R₁) и повышение напряжения конденсатора, а при размыкании - относительно медленный разряд через сопротивление R₂. Если контакт будет замыкаться достаточно часто, u_с будет постепенно повышаться и может достигнуть пороговой величины u_II(I), соответствующей такому уровню возбудимости, при котором появляются реакции на условный раздражитель (если замыкание контакта соответствует безусловному подкреплению) (II). При урежении или прекращении подачи импульсов напряжение снижается по экспоненте с постоянной времени τ₂, временная связь угасает (III-IV).

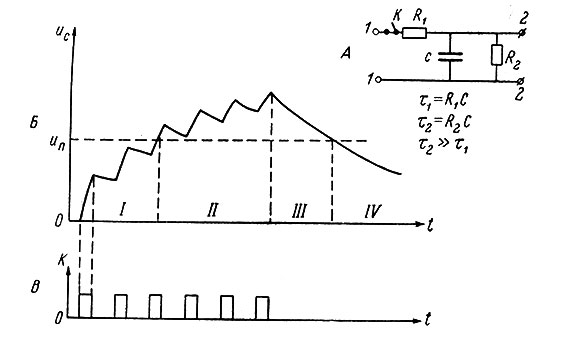
Рис. 88. Схема (A) и график работы (Б) емкостного накопительного элемента, моделирующего изменением напряжения на конденсаторе динамику временной связи (суммационного или условного рефлекса). На В показаны отметки замыкания контакта К, соответствующие подкреплению условного раздражителя

Можно продолжить дальше этот пример и осуществить такую систему автоматической телефонной станции (АТС), в которой могли бы создаваться условия для более быстрого ответа при помощи образования временной связи по типу "изменение порога чувствительности". Если набирать в подобной АТС какой-то номер несколько раз подряд, то вместо, например, трех цифр (если АТС рассчитана на 1000 номеров) достаточно будет набрать только одну (первую) и соединение произойдет. Выполняется это так: у каждого абонента должно быть реле, соединяющее его со станцией, и накопительный конденсатор. Для срабатывания реле необходимо, скажем, 15 в. При каждом наборе одной цифры накопительный конденсатор заряжается на 5 в. Первая цифра дает заряд на 100 номеров, вторая прибавит 5 в на 10 номеров, третья добавит еще 5 в на одном номере, который мы вызываем. После "набора", или "зарядки", все конденсаторы медленно разряжаются, и в зависимости от их емкости и тока утечки напряжение будет уменьшаться с определенной скоростью. Если же подряд набирать несколько раз один и тот же номер, то конденсатор этого номера будет почти полностью заряжен. В следующий раз достаточно набрать только первую цифру этой группы, как тот конденсатор, на котором уже было около 15 в, сразу включит реле, и соединение произойдет немедленно. И в последующие соединения, если набирать данный номер часто (т. е. раньше, чем успеет разрядиться емкостный элемент), каждый раз проявится временная связь, выражающаяся в повышенной чувствительности данной системы (аналогично "суммации раздражений"). Если же долгое время ее не подкреплять (зарядом), то она разрушится. Аналогично работают и такие схемы, в которых происходит сочетание индифферентного, "условного" раздражителя (свет, звук) с другим "безусловным" (например, электрическим током) и моделируется явление условного рефлекса с такими элементами, как "становление", "дифференцировка", "угашение" и т. д.

Моделирование динамики условного рефлекса (временной связи) на логических элементах сводится к реализации такого алгоритма, который обеспечивает появления действия R на "индифферентный" стимул С после сочетания его с безусловным подкреплением В. Общая схема появления реакции после появления условного или безусловного стимула (рефлекс выработан) записывается высказыванием дизъюнкции

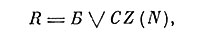
где: Z(N) - некоторая функция, имеющая значение Q, если число сочетаний меньше некоторого фиксированного числа N₀ (порога) и равное 1, если N ≥ N₀. Схема, реализующая данный алгоритм при N₀ = 1 (простейший случай), представлена на рис. 89 и работает следующим образом. Выходной элемент "или" имеет порог, равный 1, и при поступлении стимула на вход безусловного раздражителя (Б) он каждый раз выдает реакцию Р (при этом также срабатывает элемент "u" = 1). Если подается изолированно стимул (условный сигнал), то срабатывает только элемент "u" = 1, но реакции Р нет, поскольку путь к выходному элементу блокирован элементом "u" = 2 (который возбуждается только при возбуждении его обоих синапсов). В том случае, когда входные стимулы (Б и В) подаются одновременно, они возбуждают элемент "или" = 2, который имеет петлю положительной обратной связи с задержкой на 1 такт (ЛЗ = 1). Если теперь в следующий такт появится стимул В изолированно, элемент "или" = 2 возбудится, так как одновременно будет возбужден и второй синапс. Порог данного элемента как бы понижается за счет действия обратной связи. Если взять элемент "или" с порогом 1, то в таком устройстве при наличии обратной связи импульс будет циркулировать неограниченное время.

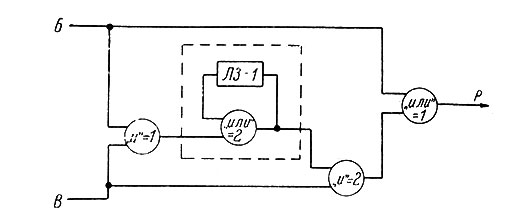
Рис. 89. Логическая схема выработки простейшего условного рефлекса с циклической памятью

В приведенной схеме выработка рефлекса происходит после первого сочетания раздражителей, а угасание - после первого же неподкрепления. Некоторым усложнением схемы - введением счетчика, выдающего импульс после n стимулов, и элемента запрета со счетчиком на m стимулов - можно моделировать соответственно выработку временной связи после n подкреплений и угасание - после m неподкреплений (Гаазе-Раппопорт, 1961). Однако и эта процедура оказывается слишком жесткой и трафаретной. Для дальнейшего приближения к реальной динамике временной связи в алгоритм образования условного рефлекса вводят случайную величину с математическим ожиданием, равным нулю, которая добавляется к показаниям счетчиков. Более сложные алгоритмы составляются для условий, когда вырабатываются цепи условных рефлексов на большое число раздражителей, при наличии большого числа состояний автомата (Брайнес, Напалков, Свечинский, 1962) и пластическим накопительным элементом (рис. 88).

Для целей синтеза автоматов с адаптивным поведением и для моделирования пластичности нервной системы К. М. Аттли (1956) предложил модель машины условной вероятности. Он поставил также вопрос о необходимости моделирования способности мозга различать и классифицировать различные состояния внешней среды. Поскольку центральный аппарат мозга не имеет прямого контакта с внешним миром, то проблема может быть сформулирована и так: каким образом в нервной системе происходит классификация и оценка всех состояний ее входов (рецепторов), особенно в тех случаях, когда число входов и возможных состояний каждого входа велико, и аппарат логических сетей делается трудно обозримым. В классификационной машине Аттли каждому возможному варианту возбуждения входов поставлен в соответствие отдельный запоминающий элемент, соединенный со всеми входами, которые он представляет (рис. 90). Все элементы идентичны и обладают двумя состояниями. Они в пределе должны соединяться со всеми входами, но тогда структура будет избыточной, так как некоторые связи будут дублироваться. Можно построить эту машину и на принципе случайного соединения элементов. Распознавание набора состояний входов (картины) производится и в данной машине мгновенно и правильно, по правилу "все или ничего", оно не улучшается и не ухудшается во время работы. Если же машина должна научиться распознавать такие отношения между картинами, как например частоту их совместного появления, то свойства элементов необходимо усложнить. Во-первых, каждый элемент должен обладать не двумя, а множеством переменных состояний для отсчета безусловной вероятности (частоты) появления данного набора. Во-вторых, нужен элемент, где производится оценка отношения безусловных вероятностей разных элементов, для получения условной вероятности совместного появления сопоставимых картин. Такой элемент, который классифицирует активность других элементов и включает в себя их наборы, называется сверхэлементом, а его набор - сверхнабором. Условную вероятность можно вычислить как разность логарифмов безусловных вероятностей.

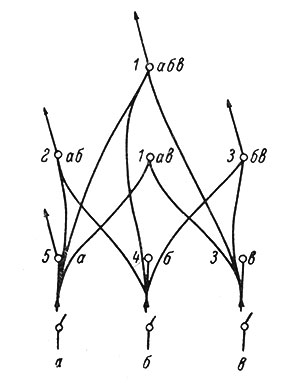
Рис. 90. Схема соединений полностью различающей классификационной машины с тремя двоичными входами

Далее А. М. Аттли рассматривает гипотетический эксперимент по образованию условных рефлексов и предлагает вычислять условную вероятность подкрепления как отношение числа подкрепленных предъявлений к общему числу подкрепленных и неподкрепленных предъявлений условного раздражителя. Следует подчеркнуть, что точно такую же формулу предложил физик Н. Романов (1935) в своей работе, выполненной в лаборатории И. П. Павлова в Институте экспериментальной медицины.

Итак, в машине условной вероятности при появлении сигналов К (безусловный раздражитель) и J (условный раздражитель), соответствующий набор должен содержать элемент, где хранится вся прошлая история событий и, в частности, условная вероятность р(J/К), которая вычисляется как разность логарифмов вероятностей р(J) и р(К) с учетом весовой функции, зависящей от времени (прошлое событие представляется меньшей величиной, чем текущее).

В машине условной вероятности осуществляются операции взаимодействия элементов между разными уровнями управления, называемые суперконтролем и субконтролем, которые подчиняются некоторым правилам. Через элементы высших уровней все группы входов соединены между собой, и активность одного или группы входов изменяет вероятность активности других входов (статистически зависимых в силу прошлого опыта). Утверждение, что два представления сходны между собой, в машине условной вероятности равносильно утверждению, что появление одного повышает вероятность появления другого.

Если для управления эффекторными механизмами достаточно оценки величины вероятности по принципу "все или ничего", то конструкцию машины можно значительно упростить, так как элемент должен иметь только два состояния и срабатывать лишь при превышении одного порогового значения. Такую машину Аттли назвал машиной "условной достоверности". Он далее писал: "Если принять, что нервная система построена по этому принципу, то становится понятно, как действие условного раздражителя может увеличить вероятность безусловного и, следовательно, безусловной реакции. Если элемент, хранящий эту вероятность, соединен через пороговое устройство с эффекторным механизмом, то увеличение вероятности безусловной реакции может привести к появлению реакции".

Представления А. М. Аттли были проверены в физиологических и психологических опытах (Ловчиков и Меницкий, 1963; Меницкий, 1964), где указываются некоторые ограничения этой модели. Далее В. М. Глушков (1964) предложил устранить некоторые недостатки машин условной вероятности и дополнить их рядом свойств, сближающих их с условнорефлекторным поведением животных, и назвал свою модель "машина условных рефлексов".

Примерами систем с пластическими связями, самоорганизующимися в процессе "обучения" или "тренировки", могут служить системы для опознавания зрительных образов - "перцептрон" (Розенблат, 1962) и "пандемониум" (Selfridge, 1959). Перцептрон (рис. 91) содержит модель сетчатки из множества фотоэлементов, на которую проектируется оптическое изображение объекта (геометрические фигуры - круг, треугольник, квадрат и т. п.). Фотоэлементы соединены в случайном порядке с множеством ассоциативных элементов, или нейроидов первого порядка, представляющих собой пороговые логические элементы (группа источников), дающих на выходе сигналы 1 или 0, и реагирующего (решающего) блока R с выходным сигналом Z (0 или 1). Связи между ассоциативными элементами и решающим блоком имеют регулируемый коэффициент передачи а, изменяющийся под влиянием обратной связи р. В простом перцептроне обучение производится с помощью "учителя". На входе появляются изображения, относящиеся к двум образам, и вначале на выходе получаются ответы (0 или 1) в случайном порядке с одинаковой вероятностью. При неправильном ответе производится "наказание", т. е. изменение коэффициентов а у той группы связей, которые действовали в данном случае. Постепенно система начинает давать правильные ответы (до 90%).

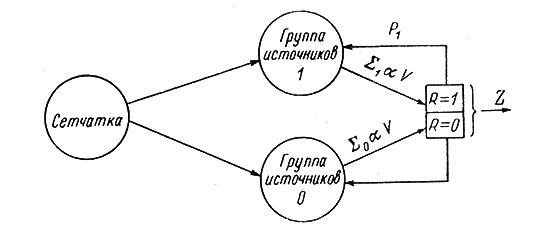
Рис. 91. Структурная схема простейшего перцептрона. Объяснение в тексте

В аналогичной модели "пандемониум" производилось обучение распознаванию точек и тире азбуки Морзе. На входе имеется n датчиков - рецепторов Д, соединенных в определенном порядке (в зависимости от характера образов) с входными усилителями ВУ и усилителями У с переменными коэффициентами усиления (рис. 92). В сумматоре происходит сравнение всех сигналов, и выходное устройство выдает сигнал. Процесс облучения состоит в том, что "учитель" отмечает ошибки, а управляющее устройство (УУ) подбирает оптимальную комбинацию величины изменяемых коэффициентов X для получения наименьшего числа ошибок (воздействие "учителя" может быть заменено соответствующими подкреплениями из внешней среды). Предполагается, что, кроме самонастройки (изменения коэффициентов усиления) в аппарате может происходить и самоорганизация - отключение слабо влияющих и подключение новых элементов на первой ступени с новыми характеристиками. Развитию исследований по обучению автоматов способствует моделирование процессов узнавания в нервной системе на универсальных вычислительных машинах (Бонгард, 1962).

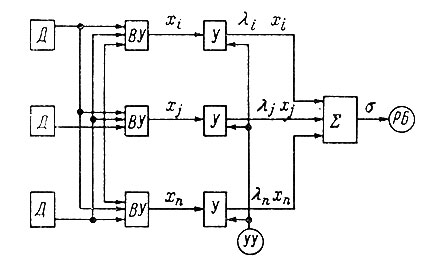
Рис. 92. Блок-схема обучающейся машины-пандемониума

По мнению У. Розенблита (1961), именно в этом отношении вычислительные машины обещают оказаться наиболее эффективными для рационального конструирования моделей поведения сетей и групп нейроноподобных элементов, или нейронов, которым приписывают некоторые свойства реальных нейронов и связывают их затем друг с другом предписанным образом. Можно исследовать поведение таких нейроидных сетей при варьировании их геометрических и специфических свойств и оценивать взаимодействия этих свойств с изменениями раздражителя и состояния. Из подобных опытов выводят обоснованные параметры функционирования этих сетей, а также представление о свойствах групп, соизмеримых с такими понятиями, как возбудимость, торможение и рефрактерность, которые по-настоящему определены лишь для одиночных элементов. Опыты такого рода дадут нам перечни моделей взаимодействия, истинность которых мы сможем проверить на реальных нервных системах. Одна из ближайших задач нейрокибернетики - попытаться свести все процессы на различных уровнях биологической организации к общим единицам измерения.