III. Логические и нейронные сети

Моделирование реакций (поведения) ансамблей, составленных из многих элементов (и тем более нервной системы в целом), с детальной имитацией всех или даже большинства свойств реального нейрона на физических моделях в настоящее время является практически неразрешимой задачей. Поэтому в нейрокибернетике, используя аппарат математической логики, анализируются для этой цели логические сети, состоящие из множества логических элементов, каждый из которых выполняет какую-либо элементарную логическую функцию, т. е. осуществляет определенную логическую зависимость между входными и выходными сигналами. Наибольшее распространение получили сети с двоичными логическими элементами, когда сигналы на выходе могут иметь только два значения (0; 1) по принципу "все или ничего". Используя правила алгебры логики, с помощью сети из двухзначных логических элементов можно представить различные логические формулы, или "высказывания", причем задача состоит в том, чтобы определить истинность или ложность сложного высказывания, полученного на выходе системы, в зависимости от истинности и ложности высказываний сигналов на входе.

Обычно высказывания обозначаются большими латинскими буквами: А, В, С, ..., а логические действия над ними с помощью значков операторов.

Утверждение (или тавтология) не имеет отдельного знака и обозначается буквой высказывания. Отрицание высказывания А (оператор "не") есть такое высказывание, которое истинно, если А ложно, и ложно, когда А истинно. Обозначается чертой "-" сверху.

Конъюнкция высказываний (оператор И, логическое умножение) - сложное высказывание, которое будет истинным только в случае, когда истинны все его составляющие (т. е. и первое, и второе и т. д.). Конъюнкция обозначается значком "∧", а в табл. 12 даны примеры для двух составляющих. В электрической цепи конъюнкция означает последовательное соединение контактов - ток течет, только если все контакты замкнуты. Дизъюнкция (оператор "или", логическое сложение) - высказывание, которое ложно, если ложны все составляющие, и истинно во всех остальных случаях (здесь значок "∨" имеет смысл союза "или" "неразделительного"). В параллельной схеме соединения контактов ток течет, если хоть один из контактов замкнут.

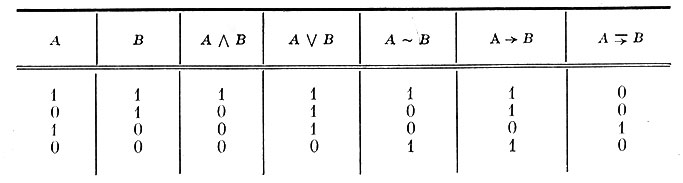
Таблица 12. Примеры конъюнкции, дизъюнкции, эквивалентности и импликации двух составляющих

Эквивалентность - "∼" - сложное высказывание, истинное в том случае, когда значения истинности составляющих высказываний одинаковы, и ложное, если они различны.

Импликация двух высказываний - А "→" В - такое сложное высказывание, которое всегда истинно, кроме случая, когда А истинно, а В ложно. Используя знак инверсии (оператор "не"), можно образовывать и другие логические высказывания. Так, например, "отрицание импликации" позволяет моделировать реакцию нейрона, имеющего возбуждающий (А) и тормозящий (В) синапсы. Сигнал на выходе появится, очевидно, только тогда, когда имеется сигнал А и нет В, иначе это условие можно представить как: (А ∧ В¯).

Число различных сложных высказываний, полученных посредством указанных логических операций из n простых высказываний, равно 2²ⁿ. В частности, для двух переменных (А и В) число различных сложных высказываний N = 2²² = 16, в которое входят и рассмотренные выше. Логической сетью называется совокупность соединенных между собой логических элементов, с помощью которой можно моделировать функции математической логики. Основные задачи теории логических сетей сводятся к анализу данной сети (определение реализуемой функции, преобразование заданной сети в алгебраически ей эквивалентную) и синтезу (по данной логической функции построить логическую сеть с минимальным числом элементов и т. д.). Логические сети являются основными функциональными устройствами цифровых вычислительных и управляющих машин. Наиболее распространенные логические сети строятся из трех типов логических элементов, выполняющих операции "и", "или", "не", с помощью которых можно реализовать любую логическую функцию.

Физическая (техническая) реализация логических элементов осуществляется различными способами. На рис. 85 показаны обозначения основных элементов на схеме (А) и их аналогии на электромеханических реле (Б) и на электронных лампах (В). Для реализации логических сетей с параметрами, зависящими от времени, используют еще два типа элементов - задержки и счетчик импульсов. Задержкой (или линией задержки) является двухполюсник, на выходе которого сигнал просто повторяет значение входного сигнала, но с запаздыванием на время задержки. Счетчиком называют трехполюсник с одним выходом и двумя входами - счет и сброс. Если счетчик на n импульсов находится в нулевом положении, а на счетный вход подается серия импульсов, то на выходе сигнал появится после прохождения n импульсов, после чего счетчик возвращается в нулевое положение. При появлении импульса на втором входе происходит сброс показаний до нулевого, после чего счет поступающих импульсов начинается снова.

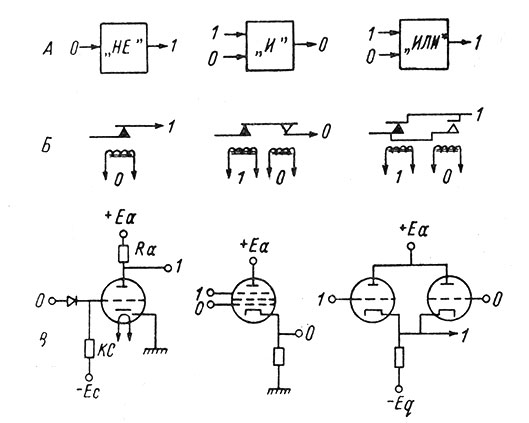
Рис. 85. Логические элементы 'не', 'и', 'или' (А) и их техническая реализация; Б - на электромагнитных реле, В - на электронных лампах

Таким образом, логическая сеть представляет собой дискретную структуру из различных логических элементов (рис. 86), соединенных между собой таким способом, что выход одного или нескольких из них является входом для другого. Часть элементов, входы которых свободны от связи с другими элементами, называются входными. Другие, не имеющие связей на выходе, называются выходными (остальные относятся к внутренним). Задать логическую сеть - значит указать состояние всех элементов в данный момент и порядок перехода из одного состояния в другое. Тогда при наличии информации о воздействии внешних сигналов на входные элементы (входной алфавит) можно определить состояние выхода в сети (выходной алфавит). Однозначно, если сеть детерминирована, и с некоторой вероятностью, если порядок переходов определен лишь с некоторой вероятностью. В абстрактной теории автоматов содержание понятий "автомат" или "машина" определяется формальным описанием того преобразования информации или состояний, которое осуществляется данным автоматом. Принято различать автоматы с бесконечной памятью (машина Тьюринга), автоматы на неограниченное число действий (при ограниченном числе различных операций) и конечные автоматы.

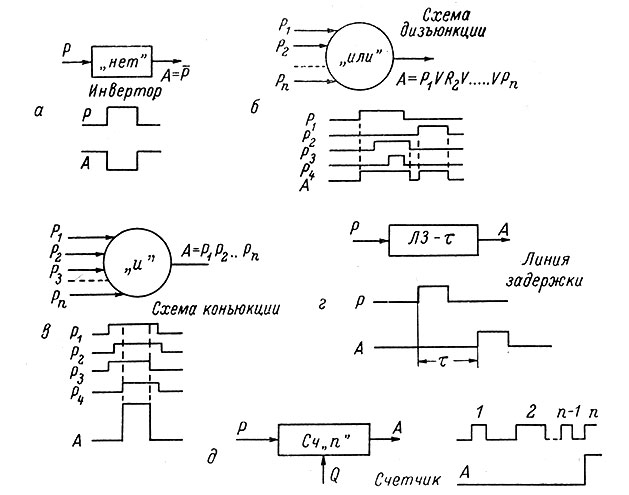
Рис. 86. Условные изображения и схема функционирования некоторых элементов логических сетей

Конечным автоматом называется логическая сеть с m входными состояниями x₁, х₂, ... х, n внутренними состояниями (q₁, q₂, ..., q_n) и k выходными состояниями (y₁, y₂, ... y_k). Время отсчитывается дискретными тактами 1, 2, 3, ... t для всех элементов одномоментно. Состояние выхода автомата в данный момент зависит от состояния входа (или внутреннего состояния) в предшествующем такте (могут быть и другие зависимости):

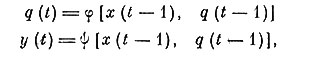
где φ и ψ - функции перехода состояний и выходов, задаваемые обычно таблицами или диаграммами переходов.

Изучение проблем синтеза конечных автоматов производится в терминах представимости событий, понимаемых как определенное множество состояний входов, которые представляются изоморфными множествами внутренних или выходных состояний. При анализе конечных автоматов решается обратная задача: по заданной таблице переходов установить, какие события представляет данный автомат. Сюда же относится задача минимизации - найти схему автомата, эквивалентного данному, но с наименьшим числом состояний. Для моделирования биологических систем представляют интерес автоматы с изменяющейся под влиянием внешних воздействий структурой. Рассмотрим процесс обучения простого автомата с линейной тактикой (Цетлин, 1961; Варшавский, Воронцова и Цетлин, 1962), имеющего несколько состояний, причем переход в то или иное состояние зависит от воздействия, которое он получает на входе от внешней среды. Воздействия среды разделяются автоматом на два класса, условно обозначенные как "штраф" и "поощрение", причем задачей обучения автомата является выработка такого "поведения", чтобы математическое ожидание штрафов было бы наименьшим (примером может служить автомат, изменяющий свои действия после "штрафа" и повторяющий их после "поощрения").

Интересно изучить поведение автомата в среде, свойства которой изменяются во времени, например, переключаются с некоторой вероятностью. Оказалось, что для каждой частоты переключений существует оптимальное число автомата (Цетлин, 1961). Наличие оптимума объясняется тем, что если среда изменяется медленно, то можно применять длинный алгоритм, который работает долго, но более точно (за счет изменения шага квантования состояний). Если же среда изменяется быстро, то такой алгоритм сработает слишком поздно. Этот результат интересно сравнить с проблемой оптимальной подвижности нервных процессов при переделке условных рефлексов. В простейшем случае полагают, что выход нейрона имеет только два состояния в соответствии с правилом "все или ничего", и эти состояния в каждый данный момент определяются однозначно состоянием его входов, действующих по такому же правилу.

На основании таких определений формального нейрона Мак Каллох и Питтс (1956) создали абстрактную модель нервной сети, которая состоит из конечного числа нейронов, связанных между собой определенным образом. Каждый нейрон соединен с соседними при помощи аксона с нервными окончаниями, которые относятся при анализе сети к следующему нейрону. Число входов (синапсов) может быть любым, но каждый синапс может быть или возбуждающим, или тормозящим. Синапсы могут иметь различный вес, определяемый специальным коэффициентом, который имеет разные знаки для возбуждающих и тормозных синапсов. Нейрон возбуждается в том случае, если сумма возбуждающих синаптических коэффициентов превышает значение порога данного нейрона, и не возбужден ни один тормозящий синапс. Нейрон называется входным или рецепторным, если ни одно нервное волокно на нем не оканчивается. Его выход определяется состоянием входов вне нервной сети в данный момент. Состояние внутренних нейронов определяется суммой синаптических влияний со стороны его входов в предыдущий момент времени, поскольку время для данной сети отсчитывается дискретными тактами, а в каждом синапсе всегда происходит временная задержка на один такт. Иными словами, состояние выхода нейрона в данный момент определяется состояниями его входов в предыдущем такте. Возбуждение тормозящего синапса исключает возбуждение нейрона в данный момент времени. Структура нервной сети неизменна. Более поздние исследования несколько изменили понятие формального нейрона. В частности, тормозной сигнал перестал быть абсолютно запрещающим, и условия возбуждения нейрона определяются разностью возбуждающих и тормозящих сигналов, которая должна превосходить некоторое число, называемое порогом данного нейрона (рис. 87). В дальнейшем появились и другие разновидности формальных нейронов, в том числе и такие, свойства которых изменяются во времени или под влиянием внешнего сигнала (Brain, 1961; Blum, 1962).

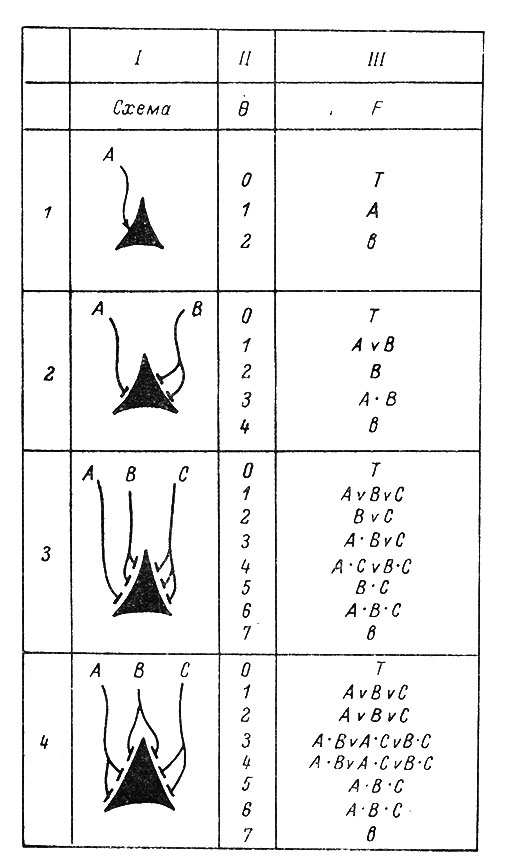
Рис. 87. Логические функции, вычисляемые различными схемами синаптических соединений при разных значениях порога

Некоторое упрощение логической нервной сети можно получить, используя однородные пороговые элементы, где появление реакции на выходе описывается функцией

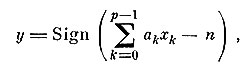
где n - порог возбуждения, а_k - вес входа (синаптическое число), а функция y получает значение 1 или 0, если выражение в скобках больше или меньше нуля.

Логический анализ пороговой модели показал возможности реализации большого числа логических функций (Варшавский, 1963) и создание систем с высокой надежностью работы (Сочивко, 1965). При очень большом числе элементов поведение (или изменение состояния всех элементов) логической сети становится весьма сложным и трудно обозримым даже в математической форме. Это привело к созданию моделей сплошных (непрерывных) возбудимых тканей, или континуальных моделей (Гельфанд и Цетлин, 1960; Балаховский, 1961; Варшавский; 1963).

Понятие возбудимой ткани можно пояснить рассмотрением нервной сети в мелком масштабе, когда ее отдельные элементы уже не различимы. В простейшем случае рассматривают изотропную ткань, которая обладает следующими свойствами. Каждая точка ткани может возбуждаться спонтанно с определенным периодом Т или под влиянием соседних возбужденных точек. После мгновенного возбуждения следует период рефрактерности (R < Т). Возбуждение может волнообразно распространяться во все стороны со скоростью, пропорциональной в данной точке ее фазе, т. е. времени, которое прошло с момента последнего возбуждения (понятно, что через зону рефрактерности волна возбуждения распространяться не может). На модели непрерывных возбудимых тканей были изучены их интересные свойства. Они способны к самосинхронизации, и отдельные участки таких тканей обладают памятью на предыдущие внешние воздействия и даже могут выполнять некоторые логические операции. Такое устройство памяти, по мнению авторов, имеет высокую надежность работы, недостижимую для дискретных моделей. Дополнительные возможности моделирования возникают, если создать анизотропную ткань, в которой направление распространения волны возбуждения поддается управлению. Континуальные модели успешно применяются для моделирования процессов синхронизации активности множества элементов в биологических однородных тканях (Гельфанд и соавт., 1962; Лукашевич, 1964).