II. Моделирование функций нейрона

Рассмотрим подробнее одну из функциональных моделей нейрона, модифицированную и детально исследованную в работе В. И. Кия и Э. К. Казимирова (1962).

Принципиальная схема модели (рис. 83) содержит так называемый задержанный, или ждущий мультивибратор на полупроводниковых триодах (транзисторах) Т₁ и Т₂, на выходе которого сигнал имеет два состояния ("все" или "ничего"). Напряжение после мультивибратора поступает на усилительный каскад (триод Т₃) и затем на эмиттерный повторитель (Т₄), который в данной схеме не несет никакой логической нагрузки и осуществляет лишь функцию согласования сопротивлений при подключении входов других нейронов сети.

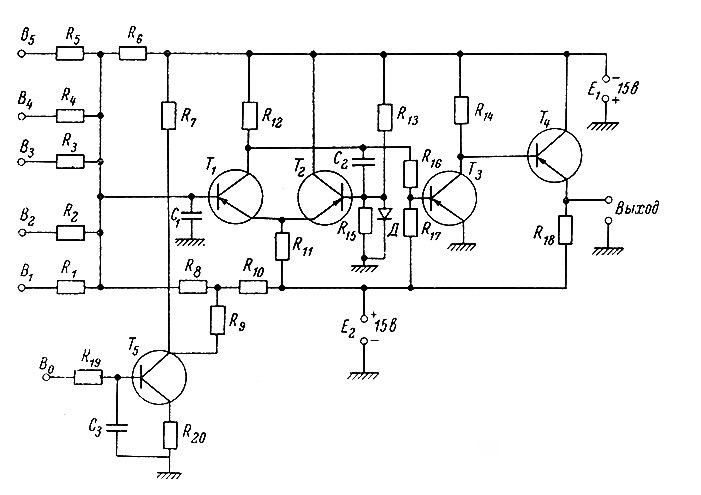
Рис. 83. Принципиальная схема модели нейрона. Объяснения в тексте

Логическая схема модели имеет пять возбуждающих сигналов (входы 1-5) и один тормозящий (6). Импульсы на всех входах имеют одинаковую полярность, но сигнал от тормозящего входа меняет полярность на усилительном каскаде (триод Т₅), и поэтому оказывается в противофазе с импульсами от возбуждающих входов, суммирующихся на конденсаторе С₁. Постоянная времени τ₁ суммирующей (интегрирующей) ячейки определяется в основном величиной С₁ и эквивалентным сопротивлением R_э входа (R₁-R₅, соединенных параллельно). При одном входном сопротивлении τ₁ равно примерно 1.5 мсек. (при подключении остальных сопротивлений τ₁ уменьшается до 0.6 мсек.).

Остальные параметры модели нейрона имеют следующие значения. Порог возбуждения определяется как минимальное напряжение на входе, при котором происходит срабатывание схемы и для данного случая составляет с учетом всех элементов входа приблизительно 5 в. Это в значительной степени превосходят пороговые значения реального нейрона (10 мв), но выбрано таким, чтобы исключить влияние нестабильности источников питания и флуктуации шумов самой схемы. Амплитуда импульса на выходе установлена таким образом, чтобы соблюдалось реальное соотношение между значением порога следующего аналогичного нейрона и величиной импульса действия в нейроне ("гарантийный фактор"). В данной модели амплитуда выходного импульса в среднем равна 15 в, т. е. гарантийный фактор взят равным 10.

Длительность выходного импульса в данной схеме зависит от времени перезаряда конденсатора С₂, которое определяется также величиной сопротивлений R₁₁-R₁₂ и приблизительно равно 0.5 мсек. (т. е. примерно столько же, сколько и в натуре). Это же время длится и период абсолютной рефрактерности модели.

Период восстановления (относительная рефрактерность) после прохождения импульса определяется временем заряда С₂, которое можно регулировать в пределах от единиц до десятков миллисекунд. Ток заряда, проходя по эмиттерному сопротивлению R₁₁, создает дополнительное напряжение смещения рабочей точки транзистора Т₁, и порог срабатывания схемы повышается. По мере уменьшения тока заряда (по экспоненте с постоянной времени τ₂) порог срабатывания возвращается к норме.

Имеющая указанные основные параметры модель позволила авторам моделировать различные функциональные особенности нейрона.

1. Латентный период и зависимость "амплитуда-длительность" входного сигнала. Как известно, возбудимые ткани характеризуются латентным периодом и минимально необходимым временем действия (существования) раздражителя при данной его силе. В данной схеме эти зависимости моделируются свойствами интегрирующей ячейки на входе. Напряжение ε(t) на конденсаторе С₁ при подаче на вход прямоугольного импульса Е₀ достаточной длительности растет во времени по экспотенциальному закону:

где τ₁ - постоянная времени входной интегрирующей ячейки. Латентный период в данной схеме задается временем нарастания напряжения до пороговой величины в зависимости от постоянной времени τ₁, однако величина подаваемого напряжения E₀; также оказывает влияние (обратная пропорциональность). Зависимость необходимой длительности от амплитуды нелинейна и сходна с гиперболическими кривыми силы-длительности для возбудимых тканей.

2. Временная и пространственная суммация. Эти эффекты моделировались подачей пары или серии импульсов с одного или нескольких входов. Подавались "подпороговые" импульсы длительностью 0.8 мсек. с изменением интервалов между ними. При интервалах менее 2.5 мсек. наблюдался эффект, подобный синаптической суммации, т. е. срабатывание схемы при суммировании подпороговых импульсов на интегрирующей входной ячейке (что зависит от соотношения постоянной времени заряда и разряда накопительного конденсатора, а также длительности и периода повторения импульсов).

В схеме не предусмотрена одновременная суммация подпороговых импульсов от разных входов, однако это возможно осуществить, слегка изменив входную цепь модели (за счет суммации тока в общем для всех входов дополнительном сопротивлении, с которого снимается напряжение для заряда конденсатора С₁).

3. Фоновая импульсная активность. При подаче на вход модели не импульсов, а постоянного напряжения на выходе наблюдается непрерывное генерирование импульсной активности (периодическое самосрабатывание схемы). Это явление в известной мере аналогично фоновой импульсной активности нейрона, подробно рассмотренной в предыдущих главах. Физические стороны этого процесса в данной схеме можно пояснить смещением рабочей точки спусковой схемы (триггера) в неустойчивую область и превращением в обычный мультивибратор. При увеличении входного напряжения по одному входу от 1.5 до 20 в частота импульсов на выходе изменяется от 100 до 400 гц, причем при подключении остальных входов частота растет быстрее.

Использование инерционной обратной связи с выхода на вход схемы позволяет уменьшить частоту импульсов до 5 в 1 сек. Интересным выводом в связи с работой над этой задачей является указание на влияния шумовых флуктуации, которые накладывают ограничение на возможность получения низких частот. Представляет поэтому интерес изучение соотношений частоты спонтанной активности реальных нейронов с величиной и характером флуктуации их возбудимости.

4. Аккомодация. Это свойство нейрона моделируется с использованием тормозного входа, имеющего отдельную интегрирующую ячейку с постоянной времени τ₃, которую можно изменять в широких пределах. Если теперь подавать один и тот же сигнал одно временно на возбуждающие и тормозной входы, то, регулируя постоянную времени и коэффициент усиления (передачи) последнего, можно демонстрировать феномены, сходные с аккомодацией, "пачковый" импульсный разряд и другие.

Соотношение постоянных времени возбуждающего τ₁ и тормозного входов τ₃ было выбрано соответственно 1.7 и 3.6 мсек. Поэтому в первые моменты времени будет проявляться действие возбуждающего входа, и при соответствующем подборе амплитуды подаваемых импульсов проявится эффект временной суммации, который затем прекращается в результате более инерционного тормозного влияния. При увеличении силы и длительности возбуждающего влияния схема может перейти в режим генерации пачек импульсов, наблюдаемых у большинства вставочных нейронов. Интересно, что на модели наблюдается и логарифмическая зависимость длительности пачки, а также числа импульсов в пачке от относительной амплитуды раздражителя (величины, показывающей, во сколько раз данное воздействие превышает пороговую величину). Длительность пачки, выраженная через параметры внешнего сигнала, и постоянных времени входов, имеет вид

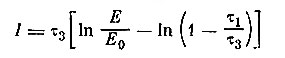
и при τ₁ << τ₃ приблизительно равна

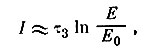
откуда видно, что длительность пачки пропорциональна величине постоянной времени тормозного входа. Эта закономерность еще не использована в биологических исследованиях.

Если постоянная времени возбуждающего входа очень мала (меньше интервалов между импульсами), то после быстрого понижения порога затем наблюдается длительное его повышение, что (при большой амплитуде возбуждающего воздействия) приводит к постепенному урежению импульсов в пачке, т. е. моделируется явление аккомодации.

В целом данная модель является весьма демонстративной для иллюстрации основных свойств нейрона. Она также дает направление для некоторых биологических экспериментов и, в частности, для изучения взаимосвязи прямых возбуждающих и тормозных влияний с постоянными времени (подвижностью, лабильностью) соответствующих синапсов. Вместе с тем эта модель не воспроизводит эффектов отдаленного (пресинаптического и дендритного) торможения и ряд других свойств нейрона во взаимодействии с остальными элементами нервной системы (Антомонов, 1965).

Существует множество разновидностей физических моделей нейрона на электронных приборах. Эти модели, использующие те же (дискретные) радиотехнические элементы, что и предыдущие схемы, позволяют более точно приблизиться к имитации различных свойств нейрона (Антомонов, 1965; Сочивко, 1965).

Другое направление в моделировании - бионическое - имеет главной целью использовать некоторые свойства нейронов для построения элементов технических адаптивных систем. Наиболее известные модели получили названия: нейромим (Джонстон, 1962), нейристор (Crane, 1962) и др.

Нейристор является элементом, совокупность которых моделирует главным образом непрерывность нервной сети или другими словами - сети с распределенными параметрами, т. е. одним из видов континуальных моделей управляющих систем. Существуют и дискретные "макеты" нейристоров на электровакуумных приборах. Особенность возбудимых сетей, составленных из нейристоров, заключается в том, что после возбуждения одного элемента он после некоторой рефрактерности возвращается в исходное состояние, а волна возбуждения переходит на соседние элементы и, распространяясь во всех направлениях вместе с волной рефрактерности, может реверберировать, взаимодействуя с отраженными волнами и образуя различные конфигурации (мозаику) возбуждений и задерживаний.

Большие надежды, возлагаемые на использование нейристоров, оправдаются в том случае, если удастся создать эти схемы в микроминиатюрном масштабе из пленок полупроводникового материала с распределенными сопротивлениями, емкостями и транзисторами.

Нейромимы представляют собой триггерные ячейки двух типов, которые использовались для моделирования сенсорных путей, проводящих световое или тактильное возбуждение (Джонстон, 1962).

Полная схема модели 100 элементов фоточувствительной матрицы ("сетчатки"). Каждый элемент соединялся с нейромимом 1-го типа (с постоянным порогом), который в свою очередь соединялся с тремя нейромимами 2-го типа, и уже следующий ряд состоял из 9, а потом снова 3 и 1 (на выходе). Таким образом, всего в схеме было 1700 нейромимов, причем ряды каждого канала, кроме входного и выходного, имели внутренние связи между элементами и между каналами. Нейромимы 2-го типа соответствовали обычным свойствам нейрона: переменный порог, суммация возбуждения и торможения на входе и реакция по типу "все или ничего" на выходе. В процессе исследования для более точного моделирования оказалось необходимым перейти от жестко детерминированного функционирования элементов к вероятностному. Для этой цели на входы нейромимов 2-го типа подавалось напряжение от генератора шумов, а выходные импульсы подбирались близкими к пороговым значениям последующего входа. Дополнительным условием было такое, что как только срабатывал один из нейромимов данного ряда, то его выходное напряжение подавалось на тормозные входы элементов этого же ряда. В данной работе исследовались взаимодействия между отдельными каналами в структуре, имеющей некоторое подобие самоорганизации. В частности, была предпринята попытка моделировать передачу сенсорного возбуждения при перемещении контрольной линии (края) по "сетчатке", изучались также "вызванные ответы", получаемые в результате наложения отдельных нервных разрядов.

Наконец, необходимо отметить еще один из путей моделирования нейронов - математический. В отличие от физических моделей, в которых основная цель состояла в имитации ими определенных биофизических параметров мембраны и ионных механизмов, в математическом моделировании задачей является описание зависимости выходных реакций (токов или потенциалов действия) от параметров входного (раздражающего) стимула. Иными словами, нейрон здесь рассматривается как электрический четырехполюсник (черный ящик), с применением традиционного в электротехнике математического аппарата дифференциальных уравнений (Антомонов и др., 1965). По материалам последней работы познакомимся подробнее с математической моделью возбуждения нерва при действии прямоугольного раздражающего электрического стимула.

Методика моделирования состояла в следующем. На основании экспериментов определялась форма кривой типичного потенциала действия нерва, которая в данном случае является функцией амплитуды Е и длительности τ раздражения х(t) = F(Е, τ, t).

В простейшем случае потенциал действия может быть представлен как решение линейного дифференциального уравнения второго порядка. В правой части такого уравнения записывается входное напряжение. Если раздражающий импульс короче, чем длится ответ нейрона, то, очевидно, необходимо составить два уравнения: одно - для времени действия входного импульса, когда в правой части будет Е₁ и второе, - когда в правой части будет нуль (в первом случае дифференциальное уравнение называется неоднородным, а во втором - однородным)

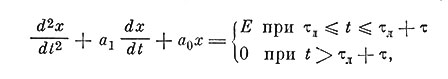
где τ_л - латентный период, α₀ и α₁ - постоянные коэффициенты у членов с нулевой и первой производными. Размерности этих коэффициентов: 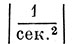и 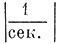. Так называемые начальные условия, т. е. значения функции в начале отсчетного времени, полагали нулевым. Интересно сопоставить данные уравнения с дифференциальным уравнением колебаний электрического контура, образованного омическим сопротивлением R, емкостью С и индуктивностью L

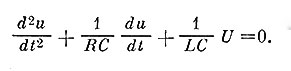
Как видно, при замене постоянных коэффициентов (имеющих одинаковые размерности) уравнения становятся идентичными. Отсюда следует, что для моделирования потенциала действия можно собрать модель из "пассивных элементов" - сопротивления, емкости и индуктивности.

Для имитации других свойств ответа реального нейрона - рефрактерности, частотного пессимума и др. - необходимо ввести дополнительные условия. Полагая, что абсолютная рефрактерность длится во время прохождения переднего фронта импульса, когда первая производная положительна 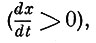, а относительная рефрактерность во время заднего фронта (когда 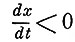), введем коэффициент Θ равный 0 в первом случае и 1 во втором. Итак, чтобы рассчитать выходной сигнал при подаче пары или серии импульсов, попадающих в фазу относительной рефрактерности (в момент времени t₁ вводится коэффициент Z = k₀ - k₁x(t₁), где k₀ - коэффициент амплитуды при нулевых начальных условиях (при t = 0) и k₁ - среднее значение амплитудного коэффициента в течение фазы относительной рефрактерности. После введения еще одного множителя ψ(Е) для нормирования величины амплитуды ответа окончательная форма уравнения модели имеет вид:

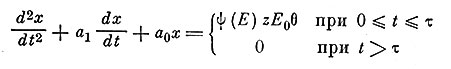
Структурная схема модели нерва приведена на рис. 84. Ниже следует пояснение этой схемы согласно Антомонову и соавторам (1965).

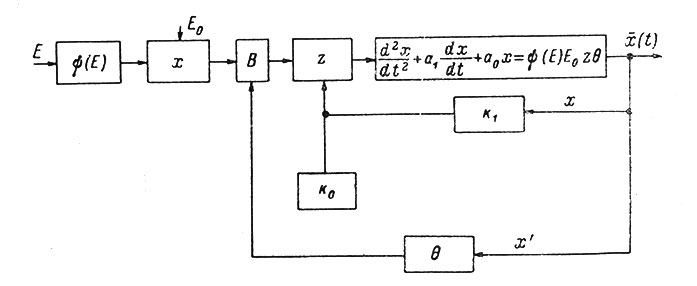
Рис. 84. Блок-схема модели нерва. Объяснения в тексте

Раздражающий стимул Е подается на нелинейный блок, где формируется функция ψ(Е), которая потом умножается на оптимальную (максимально возможную амплитуду Е₀). Полученное произведение подается на вентильное устройство В, которое или пропускает сигнал без изменения амплитуды, или не пропускает (дает нуль). В следующем блоке происходит умножение на функцию z, в начальный момент времени равную k₀. Полученный результат подается на смешанное дифференциальное звено второго порядка, описываемое приведенным выше уравнением, на выходе которого и снимается потенциал действия. Схема модели содержит две петли обратной связи с выхода системы. Первая из них - пропорциональная потенциалу действия через блок умножения k₁, суммируя произведение с коэффициентом k₀, дает величину z. Вторая петля управляет работой вентиля по закону первой производной от выходного сигнала и формирует функцию θ. В итоге данная математическая модель нерва позволяет получить потенциалы действия на одиночные и парные стимулы с учетом абсолютной и относительной рефрактерности, зависимость "сила-длительность" входного импульса в виде пороговой кривой, а также явление трансформации ритма (пессимум частоты) при подаче серии импульсов. Схема модели была с некоторыми упрощениями выполнена из типовых звеньев моделирующей установки МН-7. Использование дискретных (цифровых) и аналоговых (моделирующих) электронных вычислительных машин представляет широкие возможности для моделирования различных свойств нейрона и их взаимодействия в различном масштабе времени.